Florent Leclercq

Chargé de recherche CNRS, Institut d'Astrophysique de Paris


Blog

Algorithms for likelihood-free cosmological data analysis

25-04-2019

Overview

The extraction of physical information from wide and deep astronomical surveys relies on statistical techniques to compare models and observations. A common scenario in cosmology is when we can generate synthetic data through forward simulations, but cannot explicitly formulate the likelihood of the model. The generative process can be extremely general (a noisy non-linear dynamical system involving an unrestricted number of latent variables) and is often computationally expensive. Likelihood-free inference (LFI) provides a framework for performing Bayesian inference in this context, by replacing likelihood calculations with data model evaluations. In its simplest form, LFI takes the form of likelihood-free rejection sampling (LFRS), which tends to be (i) extremely expensive, since many simulated data sets get rejected, and (ii) very limited in the number of parameters that can be treated.

In two recent articles, we presented methodological advances, aiming at fitting cosmological data with "black-box" numerical models. Each of them addresses one of the shortcomings of LFRS. The first approach, BOLFI, is intended for specific cosmological models (with \(n \lesssim 10\) parameters) and a general exploration of parameter space. It combines Gaussian process regression of the distance between observed and simulated data with Bayesian optimization. As a result, the number of required simulations is reduced by several orders of magnitude with respect to LFRS. The second approach, SELFI, allows the inference of \(n \gtrsim 100\) parameters (as is necessary for a model-independent parametrisation of theory) while assuming stronger prior constraints in parameter space. It relies on a Taylor expansion of the simulator to build an effective posterior distribution. The resulting algorithm allows LFI in much higher-dimensional settings than LFRS.

Likelihood-free inference of black-box data models

Simulator-based statistical models are usually given in terms of numerical "black-boxes". They provide realistic predictions for artificial observations when provided with all necessary input parameters. These consist of target parameters as well as nuisance parameters such as initial phases, noise realisation, sample variance, etc. This "latent space" can often be hundred-to-multi-million dimensional. Once all input parameters are fixed, the black-box typically consists of a simulation step and a data compression step. Black-box models can be written in a hierarchical form and conveniently represented graphically (figure 1).

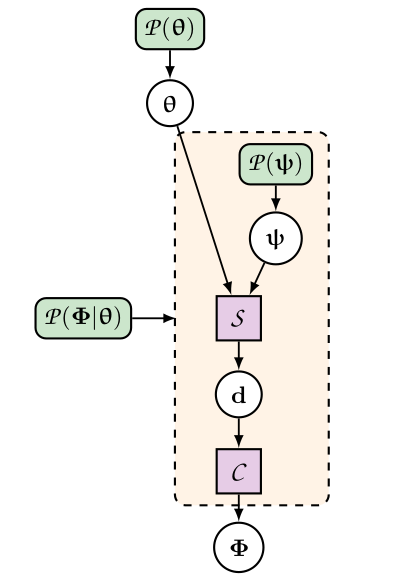Hierarchical representation of a black-box data modelFigure 1: Hierarchical representation of a typical black-box data model. The rounded green boxes represent probability distributions and the purple square represent deterministic functions. For more details, see figure 1 in Leclercq et al. 2019 [3].

The goal of LFI is to find suitable approximations that allow an estimation of the probability distribution of target parameters conditional on observed data summaries, using only black-box evaluations.

BOLFI: Bayesian Optimisation for Likelihood-Free Inference

BOLFI (Bayesian Optimisation for Likelihood-Free Inference [1,2]) is a cutting-edge machine learning algorithm for LFI under the constraint of a very limited simulation budget (typically a few thousand), suitable when the problem has a sufficiently small number of target parameters (\(n \lesssim 10\)). Conventional approaches such as LFRS generally require too many simulations, due to their lack of knowledge about how the parameters affect the distance between observed and simulated data. As a response, BOLFI combines Gaussian process regression of this distance to build a surrogate surface with Bayesian Optimisation to actively acquire training data (figure 2).

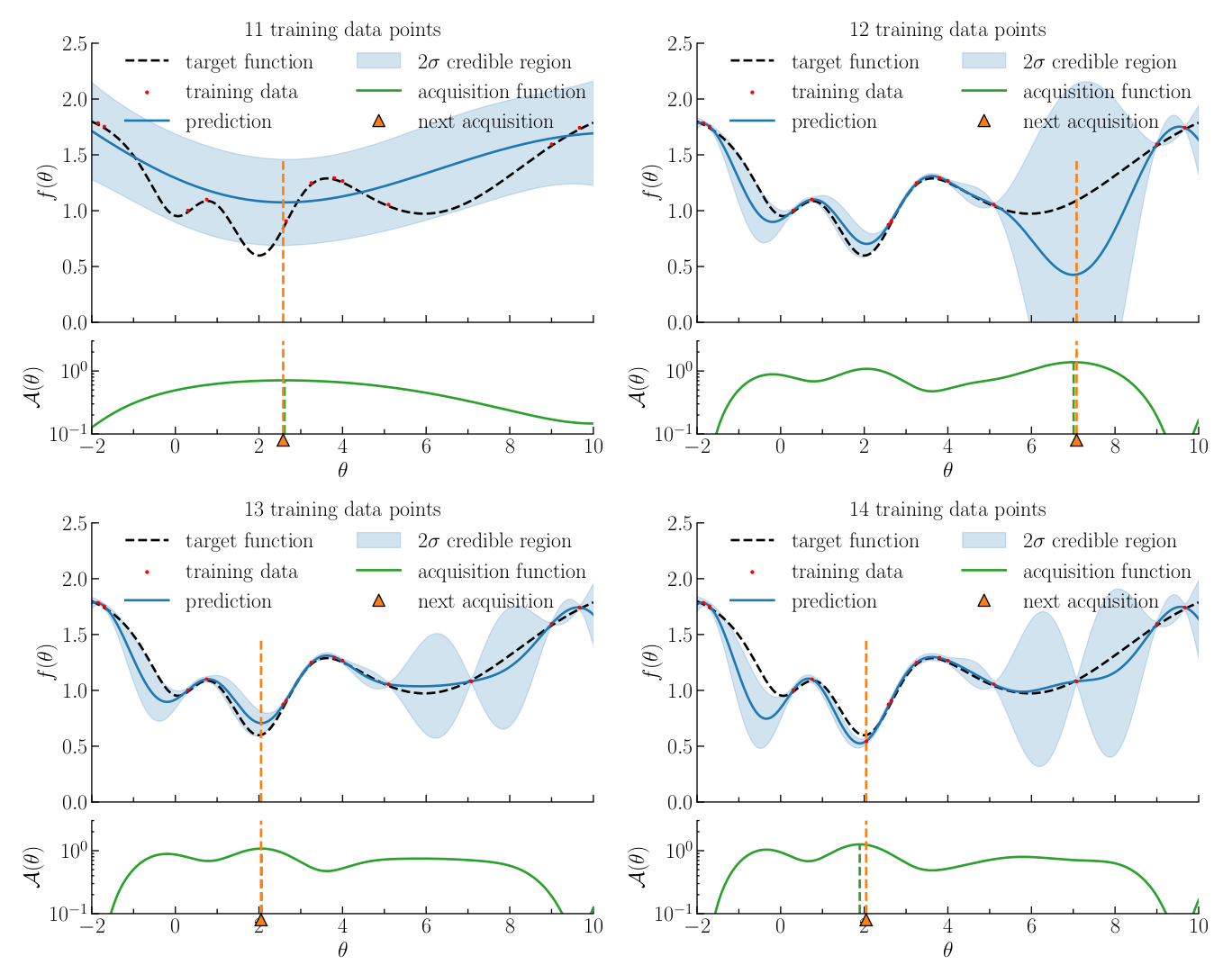Bayesian optimizationFigure 2: Illustration of four consecutive steps of Bayesian optimisation to learn a test function. For each step, the top panel shows the training data points (red dots) and the Gaussian process regression (blue line and shaded region). The bottom panel shows the acquisition function (solid green line). The next acquisition point, i.e. where to run a simulation to be added to the training set, is shown in orange. For more details, see figure 4 in Leclercq 2018 [2].

The target parameter space is explored efficiently and in all generality. We extended the method to use the optimal acquisition function for the purpose of minimising the expected uncertainty in the approximate posterior density, in the parametric approach to likelihood approximation. As a result, the number of required simulations is typically reduced by two to three orders of magnitude, and the proposed acquisition function produces more accurate posterior approximations, as compared to LFRS.

SELFI: Simulator Expansion for Likelihood-Free Inference

Another limitation of conventional approaches to LFI is their inability to scale with the number of target parameters. In order to address problems of high-dimensional inference from black-box data models, we introduced SELFI (Simulator Expansion for Likelihood-Free Inference [3]). Our approach builds upon a novel effective likelihood and upon the linearisation of the simulator around an expansion point in parameter space. The workload with SELFI consists of evaluating the covariance matrix and the gradient of data summaries at the expansion point (figure 3). Contrary to likelihood-based Markov Chain Monte Carlo (MCMC) techniques and to BOLFI, it is fixed a priori and perfectly parallel.

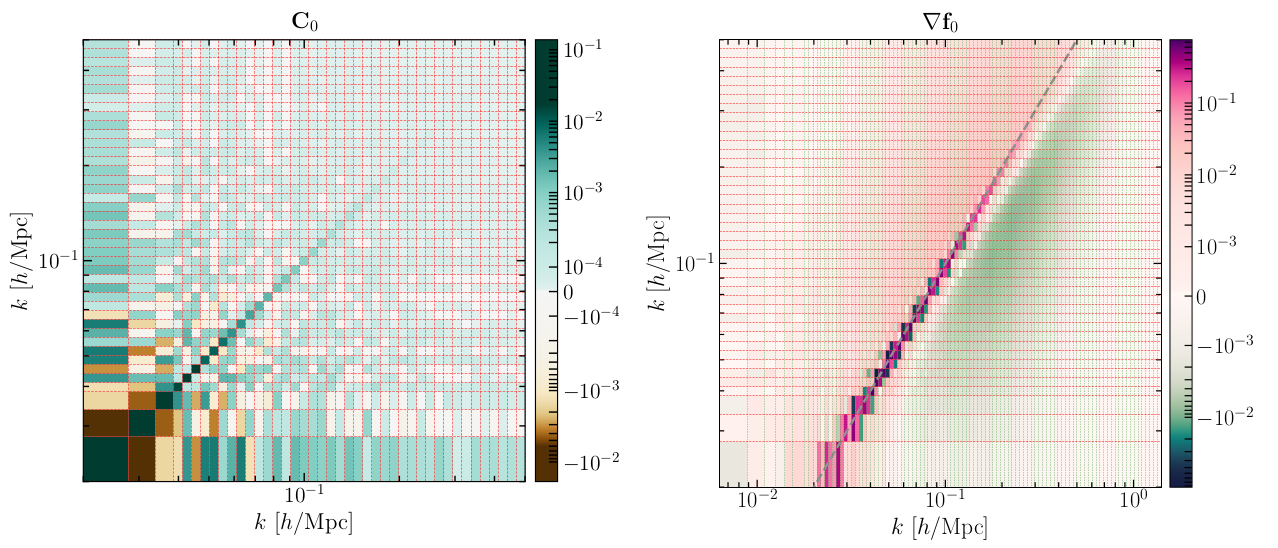Covariance and gradient of the black-boxFigure 3: Covariance matrix (left) and gradient (right) of data summaries at the expansion point, evaluated through black-box realisations only. These are the only two ingredients necessary to apply SELFI. For more details, see figures 6 and 7 in Leclercq et al. 2019 [3].

The effective posterior of the target parameters is then obtained through simple "filter equations," the form of which is analogous to a Wiener filter. SELFI allows the solution of inference tasks from black-box data models, in much higher dimension than conventional approaches to LFI.

Cosmological applications: key results

In respective papers, we presented the first applications of BOLFI and SELFI to cosmological data analysis.

Supernova cosmology with BOLFI

We applied BOLFI to the inference of cosmological parameters from the Joint Lightcurve Analysis (JLA) supernovae data. The model contains two cosmological parameters (the matter density of the Universe \(\Omega_m\) and the equation of state of dark energy \(w\)) and four nuisance parameters, which are marginalised over. The posterior contours obtained with MCMC, LFRS, and BOLFI are represented in figure 4.

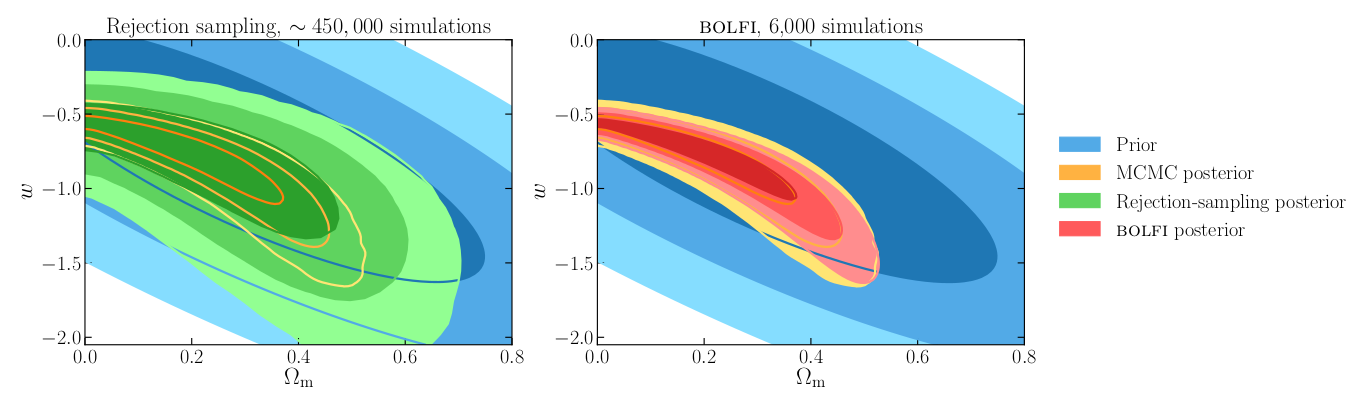Supernova cosmology with BOLFIFigure 4: Prior and posterior distributions for the joint inference of the matter density of the Universe, \(\Omega_m\), and the dark energy equation of state, \(w\), from the JLA supernovae data set. BOLFI (red posterior) reduces the number of necessary simulations by two orders of magnitude with respect to LFRS (green posterior) and three orders of magnitude with respect to MCMC (orange posterior). For more details, see figure 7 in Leclercq 2018 [2].

As can be observed, BOLFI is able to precisely recover the true posterior with as few as 6,000 simulations, which constitutes a reduction by two orders of magnitude with respect to LFRS and three orders of magnitude with respect to MCMC. This reduction in the number of required simulations accelerates the inference massively.

Primordial power spectrum and cosmological parameters inference with SELFI

We applied SELFI to a realistic synthetic galaxy survey, with a data model accounting for physical structure formation and incomplete and noisy observations. This data model is provided by the publicly-available Simbelmynë code, a hierarchical probabilistic simulator of galaxy survey data.[4] Through this application, we showed that the use of non-linear numerical models allows the galaxy power spectrum to be fitted up to at least \(k_\mathrm{max} = 0.5~h/\mathrm{Mpc}\), which represents an increase by a factor of \(\sim~5\) in the number of modes used, with respect to traditional techniques. The result is an unbiased inference of the primordial power spectrum (living in \(n =100\) dimensions) across the entire range of scales considered, including a high-fidelity reconstruction of baryon acoustic oscillations (figure 5).

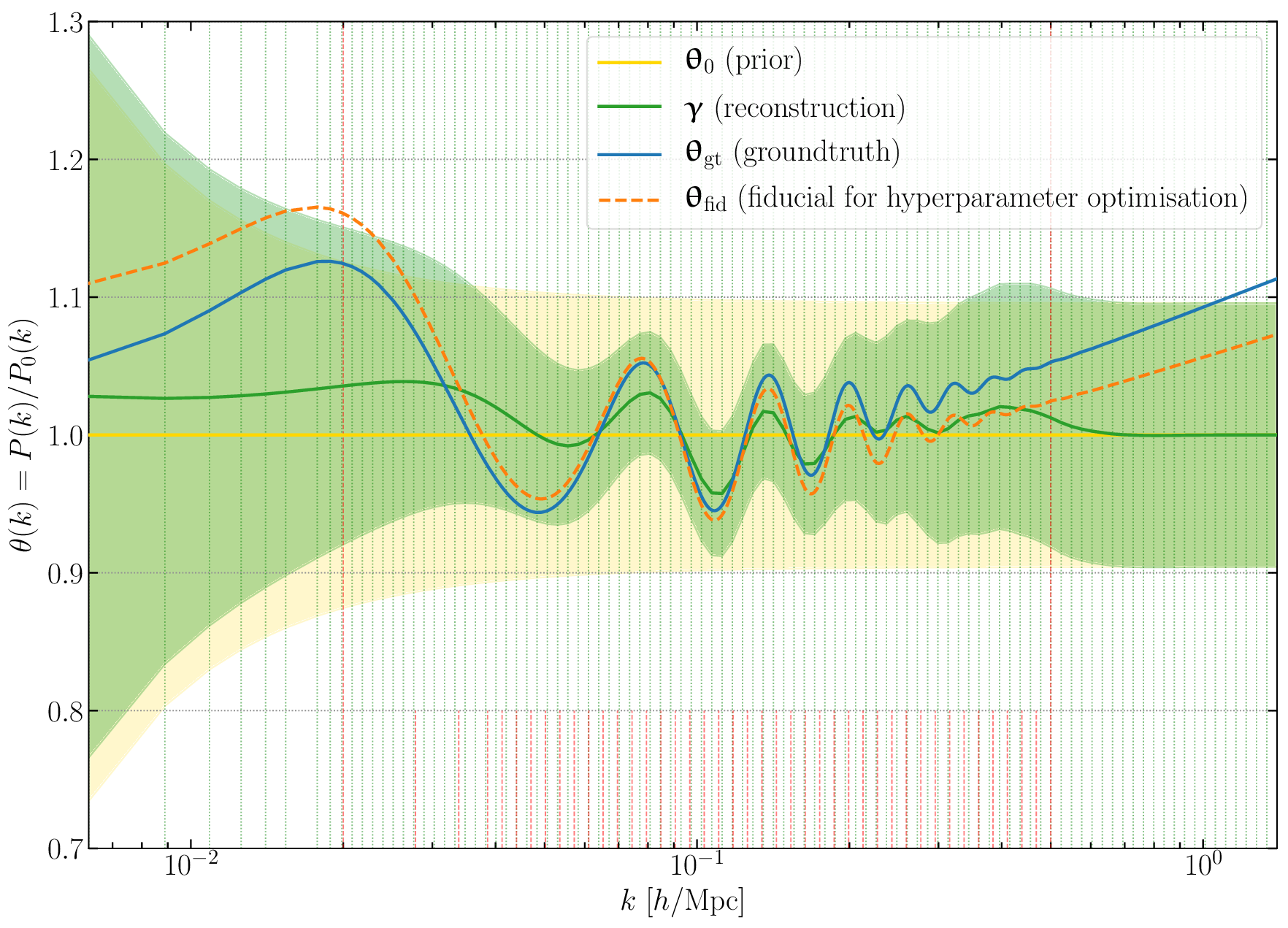Primordial power spectrum reconstruction with SELFIFigure 5: Primordial power spectrum inference with SELFI from a realistic synthetic galaxy survey. In spite of survey complications which limit the information captured, the inference is unbiased and the signature of baryon acoustic oscillations is well reconstructed up to \(k \approx 0.3~h/\mathrm{Mpc}\), with 5 inferred acoustic peaks, result which could be improved using more volume (this analysis uses \((1~\mathrm{Gpc}/h)^3\)). For more details, see figure 10 in Leclercq et al. 2019 [3].

The primordial power spectrum can be seen as a largely agnostic and model-independent parametrisation of theory, relying only on weak assumptions (isotropy and gaussianity). Using the linearised black-box, it can be easily translated a posteriori to constraints on specific cosmological models without (or with minimal) loss of information. For instance, constraints on the parameters of the standard cosmological model, for two different synthetic data realisations (with different input cosmologies, phase and noise realisations), are shown in figure 6.

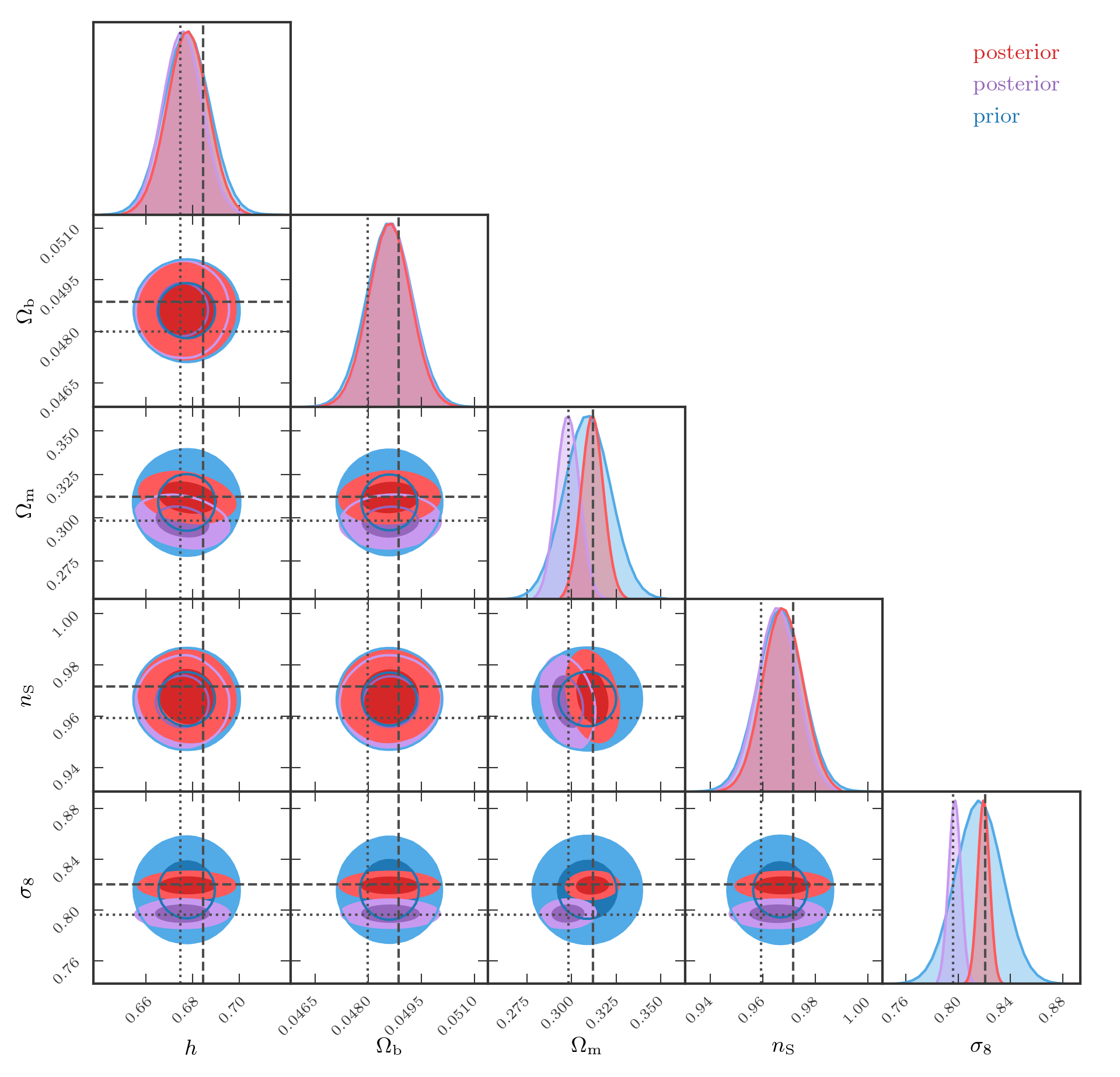Inference of cosmological parameters with SELFIFigure 6: Cosmological parameter inference using a linearised black-box model of galaxy surveys. The prior is shown in blue, and the effective posteriors for two different data realisations are shown in red and green.

We therefore obtain an unbiased and robust measurement of cosmological parameters.

References and links